Basic Mathematical Symbols
These are just a few basic mathematical symbols with their meanings and examples. Mathematics is a vast field with many more symbols and concepts to explore.
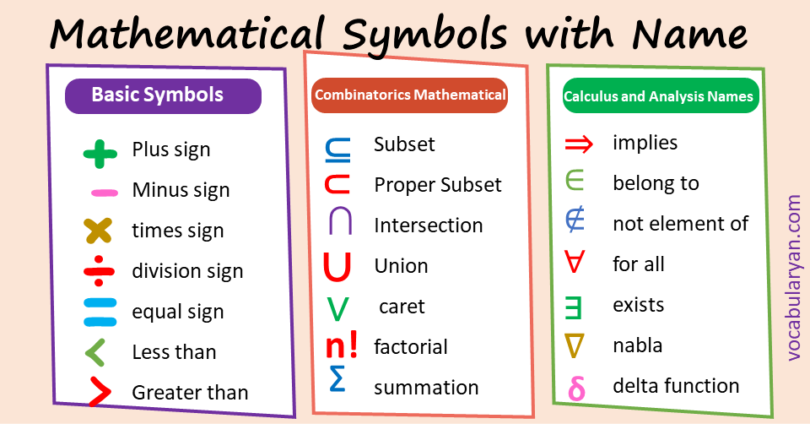
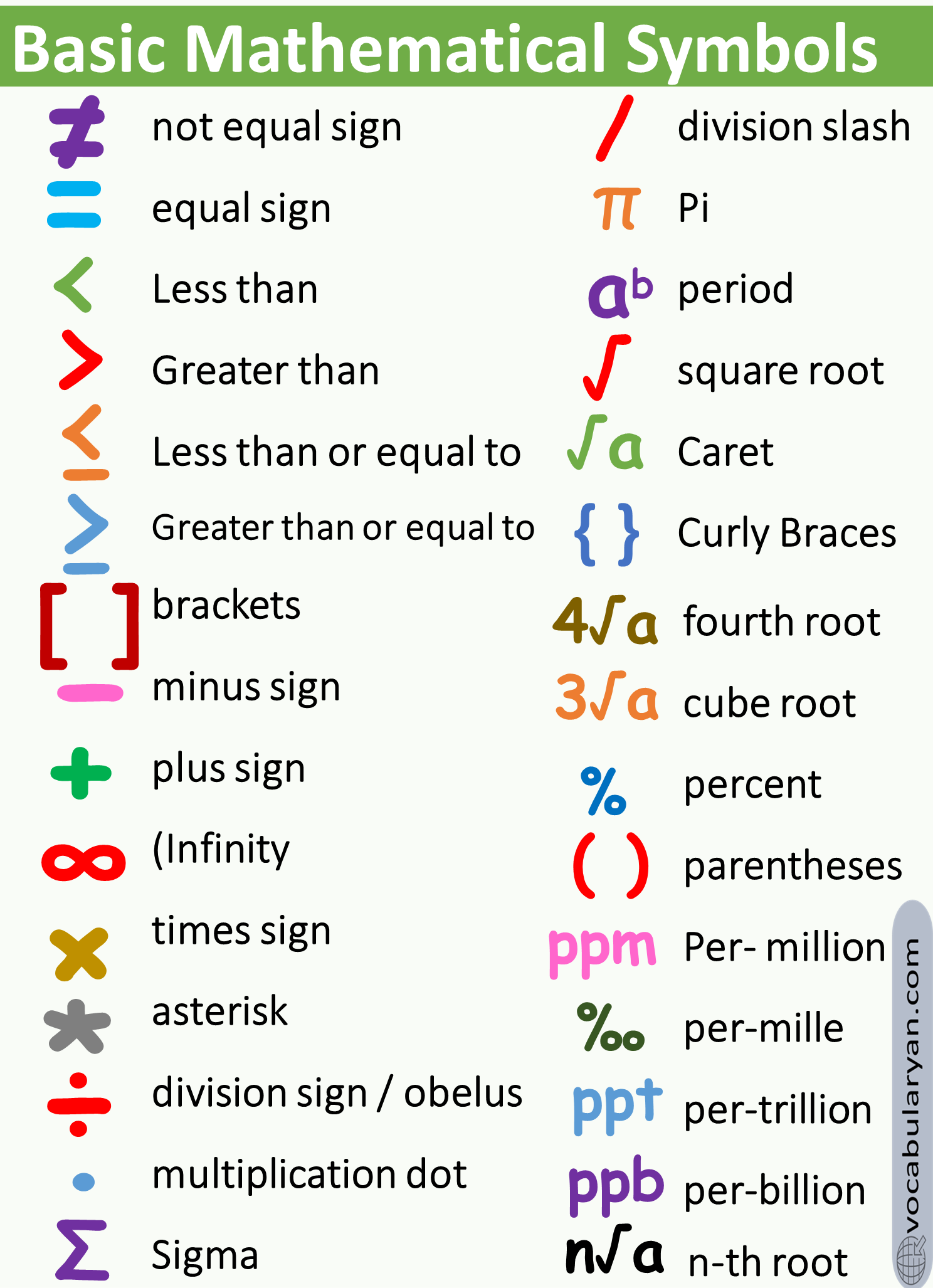
+ (Plus):
Meaning: Addition or positive value.
Example: 3 + 5 = 8
– (Minus):
Meaning: Subtraction or negative value.
Example: 10 – 4 = 6
× (Multiplication):
Meaning: Multiplication of two numbers.
Example: 2 × 6 = 12
÷ (Division):
Meaning: Division of two numbers.
Example: 18 ÷ 3 = 6
= (Equals):
Meaning: Indicates equality between two expressions.
Example: 7 + 3 = 10
< (Less Than):
Meaning: Indicates that one value is smaller than another.
Example: 5 < 8
> (Greater Than):
Meaning: Indicates that one value is larger than another.
Example: 10 > 7
≤ (Less Than or Equal To):
Meaning: Indicates that one value is smaller than or equal to another.
Example: 4 ≤ 4
≥ (Greater Than or Equal To):
Meaning: Indicates that one value is larger than or equal to another.
Example: 9 ≥ 6
( ) (Parentheses):
Meaning: Used to group expressions or indicate the order of operations.
Example: (2 + 3) × 4 = 20
[ ] (Square Brackets):
Meaning: Can be used for various purposes, like representing intervals or matrices.
Example: [1, 5] represents the interval from 1 to 5.
{ } (Curly Braces):
Meaning: Often used to represent sets in mathematics.
Example: {2, 4, 6} represents a set of even numbers.
√ (Square Root):
Meaning: Represents the square root of a number.
Example: √9 = 3
^ (Exponentiation):
Meaning: Indicates raising a number to a certain power.
Example: 2^3 = 8
% (Percent):
Meaning: Represents a fraction out of 100.
Example: 25% means 25 out of 100.
π (Pi):
Meaning: A mathematical constant representing the ratio of a circle’s circumference to its diameter.
Example: Circumference = 2πr (where r is the radius of the circle)
Σ (Sigma):
Meaning: Represents summation in mathematics.
Example: Σn from 1 to 5 = 1 + 2 + 3 + 4 + 5 = 15
∞ (Infinity):
Meaning: Represents an unbounded, limitless value.
Example: 1/∞ approaches zero.
Combinatorics Symbols
These symbols are essential in combinatorics for expressing and calculating various arrangements, selections, and other counting-related problems.
n! (Factorial):
Meaning: Represents the product of all positive integers from 1 to n.
Example: 5! = 5 × 4 × 3 × 2 × 1 = 120
nPr (Permutation):
Meaning: Represents the number of ways to arrange r objects from a set of n distinct objects, where order matters.
Example: 5P2 = 5! / (5 – 2)! = 20 (number of ways to arrange 2 objects from 5)
nCr (Combination):
Meaning: Represents the number of ways to choose r objects from a set of n distinct objects, where order does not matter.
Example: 5C2 = 5! / (2! * (5 – 2)!) = 10 (number of ways to choose 2 objects from 5)
∑ (Summation):
Meaning: Represents the summation of a sequence of terms.
Example: ∑(i = 1 to 5) i = 1 + 2 + 3 + 4 + 5 = 15
|A| (Cardinality):
Meaning: Represents the number of elements in a set A.
Example: If A = {2, 4, 6}, then |A| = 3
⊆ (Subset):
Meaning: Represents that one set is a subset of another set.
Example: A ⊆ B (set A is a subset of set B)
⊂ (Proper Subset):
Meaning: Represents that one set is a subset of another set, but not equal to it.
Example: A ⊂ B (set A is a proper subset of set B)
∩ (Intersection):
Meaning: Represents the intersection of two sets, containing elements present in both sets.
Example: A ∩ B (intersection of sets A and B)
∪ (Union):
Meaning: Represents the union of two sets, containing all elements present in either or both sets.
Example: A ∪ B (union of sets A and B)
!n (Subfactorial):
Meaning: Represents the number of derangements of n objects, i.e., permutations where no object appears in its original position.
Example: !4 = 9 (number of derangements of 4 objects)
P(n, r):
Meaning: Represents the number of permutations of r objects chosen from n distinct objects.
Example: P(7, 3) = 7P3 = 210 (number of permutations of 3 objects from 7)
C(n, r):
Meaning: Represents the number of combinations of r objects chosen from n distinct objects.
Example: C(5, 2) = 5C2 = 10 (number of combinations of 2 objects from 5)
Calculus and Analysis Symbol Names
∫ (Integral):
Meaning: Represents the concept of integration, which is used to calculate areas under curves and find antiderivatives.
Example: ∫(2x) dx = x^2 + C (where C is the constant of integration)
d/dx (Derivative):
Meaning: Represents differentiation, which measures the rate of change of a function with respect to its variable.
Example: If f(x) = 3x^2, then d/dx[f(x)] = 6x.
∂ (Partial Derivative):
Meaning: Represents a derivative of a function with respect to one of its many variables, keeping other variables constant.
Example: ∂f(x, y)/∂x represents the partial derivative of the function f with respect to x.
lim (Limit):
Meaning: Represents the behavior of a function as it approaches a certain value.
Example: lim(x → 0) (sin(x)/x) = 1 (sine of zero divided by zero equals 1 as x approaches 0)
∇ (Nabla):
Meaning: Represents the del operator, used in vector calculus to calculate derivatives, gradients, and more.
Example: ∇(f) represents the gradient of the scalar function f.
∀ (For All):
Meaning: Represents a universal quantifier, indicating that a statement holds for all elements in a set.
Example: ∀x ∈ ℝ, x^2 ≥ 0 (for all real numbers x, the square is greater than or equal to zero)
∃ (Exists):
Meaning: Represents an existential quantifier, indicating that there exists at least one element in a set satisfying a certain property.
Example: ∃x ∈ ℝ, x^2 = 9 (there exists a real number x whose square is 9)
⇒ (Implies):
Meaning: Represents logical implication, indicating that one statement implies another.
Example: If A, then B is represented as A ⇒ B.
∈ (Element of):
Meaning: Represents that an element belongs to a set.
Example: x ∈ {1, 2, 3} (x is an element of the set {1, 2, 3})
∉ (Not an Element of):
Meaning: Represents that an element does not belong to a set.
Example: x ∉ {4, 5, 6} (x is not an element of the set {4, 5, 6})
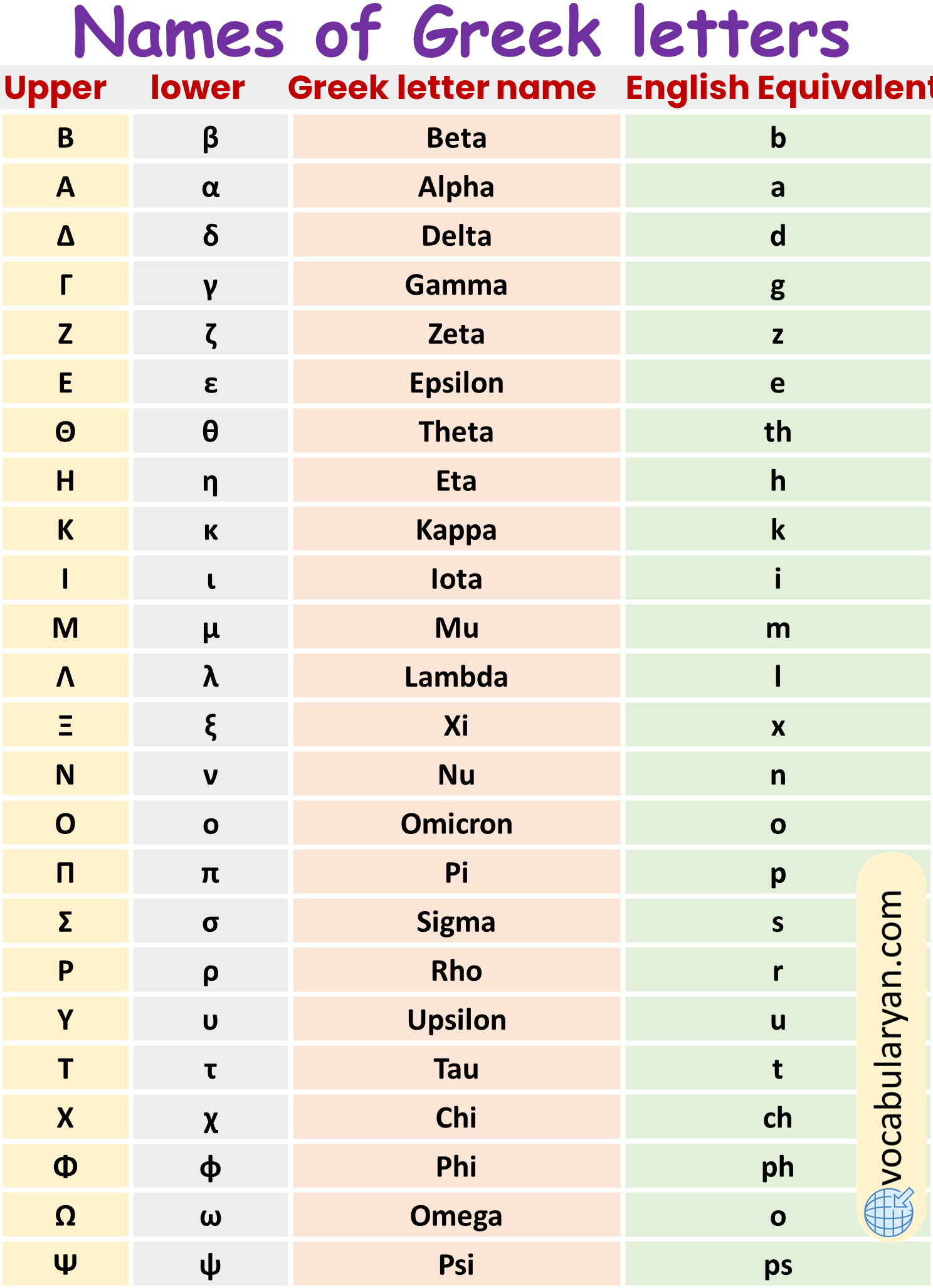
Greek Alphabet Letters Used in Maths
The Greek alphabet is widely used in mathematics and science to represent various variables, constants, and concepts. Here are some of the Greek letters commonly used in mathematics and their corresponding names and symbols:
Alpha (Α, α):
Symbol: α
Commonly used as a variable or to represent angles.
Beta (Β, β):
Symbol: β
Often used as a variable in mathematics and physics.
Gamma (Γ, γ):
Symbol: γ
Used for various purposes, including representing the gamma function and Lorentz factors in physics.
Delta (Δ, δ):
Symbol: δ
Represents differences or changes in variables. Also used in calculus to represent infinitesimal changes.
Epsilon (Ε, ε):
Symbol: ε
Commonly used to denote small positive quantities, such as in limits and epsilon-delta proofs.
Zeta (Ζ, ζ):
Symbol: ζ
Occurs in various mathematical contexts, including number theory.
Eta (Η, η):
Symbol: η
Used in mathematics, physics, and engineering contexts.
Theta (Θ, θ):
Symbol: θ
Often used to represent angles and is also commonly seen in trigonometry and calculus.
Iota (Ι, ι):
Symbol: ι
Used as a variable in mathematics.
Kappa (Κ, κ):
Symbol: κ
Appears in various mathematical and scientific contexts.
Lambda (Λ, λ):
Symbol: λ
Used to represent wavelengths in physics and eigenvalues in linear algebra.
Mu (Μ, μ):
Symbol: μ
Commonly used to represent coefficients of friction and micro-units in metric measurements.
Nu (Ν, ν):
Symbol: ν
Used in physics and other scientific fields.
Xi (Ξ, ξ): Symbol: ξ
Appears in mathematics and engineering contexts.
Pi (Π, π):
Symbol: π
Represents the ratio of a circle’s circumference to its diameter. Also used in trigonometry and calculus.
Rho (Ρ, ρ):
Symbol: ρ
Used to represent densities and resistivities.
Sigma (Σ, σ/ς):
Symbol: σ (lowercase), Σ (uppercase)
Used for summation in mathematics and also represents standard deviation in statistics.
Tau (Τ, τ):
Symbol: τ
Used in mathematics and physics.
Upsilon (Υ, υ):
Symbol: υ
Appears in various scientific contexts.
Phi (Φ, φ):
Symbol: φ
Used in mathematics and engineering, often representing the golden ratio.
Chi (Χ, χ):
Symbol: χ
Occurs in various mathematical and scientific contexts.
Psi (Ψ, ψ):
Symbol: ψ
Used in mathematics, physics, and psychology.
Omega (Ω, ω):
Symbol: ω
Often used to represent angular velocity and the last element in sets.
You May Also Like






Leave a Comment